Na ile trójkątów o rozłącznych wnętrzach można podzielić kwadrat? Na ile trójkątów o rozłącznych wnętrzach i jednakowych polach można podzielić kwadrat?
Na ile trójkątów o rozłącznych wnętrzach można podzielić kwadrat?
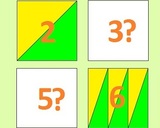
Łatwo zauważyć, że na dowolną liczbę (oczywiście większą od 1). Poniższe rysunki przedstawiają podział kwadratu na 2, 3, 4, 5 trójkątów. Podziały można kontynuować.
Tak otrzymane trójkąty mają dodatkową własność: każde dwa z nich są podobne. Udało nam się więc nie tylko rozstrzygnąć postawiony problem, ale nawet uzyskać silniejszy rezultat.
Skoro tak łatwo poszło, to postawmy trudniejszy problem: na ile trójkątów o rozłącznych wnętrzach i jednakowych polach można podzielić kwadrat?
Po chwili zastanowienia stwierdzamy, że dla każdej liczby parzystej istnieje taki podział: jeśli podzielimy kwadrat na n przystających prostokątów i poprowadzimy w każdym z nich przekątną, otrzymamy podział na 2n trójkątów, które nie tylko mają równe pola, ale nawet są przystające. Oto rysunki dla n = 1, 2, 3, 4:
Natomiast próby podzielenia kwadratu na 3 lub 5 trójkątów mających jednakowe pola i rozłączne wnętrza, wielu osobom kończyły się niepowodzeniami, aż w 1970 r. Paul Monsky udowodnił, że każda taka próba musi zakończyć się niepowodzeniem, bo taki podział na nieparzystą liczbę części nie jest możliwy (tytułowe twierdzenie).
Dowód jest dość skomplikowany i, można powiedzieć, sensacyjny. Używa się w nim m.in. pewnego twierdzenia z teorii grafów oraz tzw. waluacji p-adycznych (funkcji używanych w teorii ciał i algebraicznej teorii liczb), podczas gdy problem sformułowany jest w języku geometrii. Dowodu nie będziemy tu omawiać, można go znaleźć w oryginalnej pracy Monsky’ego (napisanej bardzo zwięźle):
On dividing a square into triangles, The American Mathematical Society, Vol. 77, No. 2/1970, pp. 161-164 lub kilku dostępnych w internecie (w jez. angielskim lub rosyjskim) bardziej obszernych opracowaniach.
Z rozwiązywaniem otwartych problemów w matematyce często jest tak, że gdy ktoś już odkryje rozwiązanie, zaczynają pojawiać się następne, prostsze od tego pierwszego. W tym przypadku jest inaczej. Nie jest znany elementarny, ani w ogóle żaden istotnie inny dowód.
Tekst: Krzysztof Kamiński


