Oto zadanie matematyczne, mimo że w pierwszej chwili wydawałoby się, że to geografia. Ilu minimalnie kolorów należy użyć na mapie, jeżeli pola o jednym kolorze, nie mogą ze sobą sąsiadować? Trzech, czterech, czy pięciu? Jak Wam się wydaje?
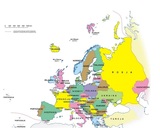
Poniżej zamieszczamy mapę polityczną Europy, równie dobrze można wziąć mapę administracyjną dowolnego kraju (z podziałem na województwa/regiony/stany).
Jak widzimy, mapa jest kolorowa – użyto kilku kolorów, każde państwo jest pomalowane, ale niektóre kolory się powtarzają (np. dla Niemiec i Finlandii, Polski i Belgii, Białorusi i Szwecji). Ale mimo to mapa jest czytelna – jest tak dlatego, że kraje sąsiadujące ze sobą malowane są różnymi kolorami. Dopuszcza się więc powtarzanie kolorów, nie wolno malować tym samym kolorem sąsiadujących powierzchni.
Ryc. Aotearoa,
źródło: http://commons.wikimedia.org/wiki/File:Europa-mapa_polityczna.png?uselang=pl
Gdzie w tym jest matematyka? Otóż matematycznym problemem jest znalezienie odpowiedzi na pytanie: ilu co najmniej kolorów należy użyć, aby pokolorować dowolną mapę polityczną, w taki sposób, by żadne dwa sąsiadujące ze sobą kraje nie miały tego samego koloru?
Takie pytanie zadawano już dawno, oryginalne źródło problemu nie jest chyba znane. Wiadomo jednak, że w 1840 roku August Ferdinand Möbius, niemiecki matematyk, postawił hipotezę, że cztery kolory zawsze wystarczą. Niezależnie od Möbiusa, tę samą hipotezę sformułowali później Francis Guthrie i August De Morgan. Żaden z nich nie potrafił tego udowodnić. Podejmowane przez różnych matematyków próby dowodu okazywały się nieskuteczne, a w kilku opublikowanych dowodach znaleziono luki lub błędy. Z drugiej strony nikomu nie udawało się znaleźć kontrprzykładu (tzn. przykładu mapy niedającej się pomalować czterema kolorami – nawet bardzo skomplikowane udawało się pomalować, nie nadając tych samych barw sąsiadującym powierzchniom). Nie wątpiono więc w prawdziwość tej hipotezy.
Poniżej przedstawiamy mapę: Okręgi wyborcze do Sejmu i Senatu Rzeczpospolitej Polskiej w 2007 roku, do której pomalowania mimo wielu wydzielonych powierzchni, wystarczyły cztery kolory.
Redakcja i kartografia: Peter G. Ochman, opracowanie: www.mapy.pl, źródło: http://www.mapy.pl/
Dopiero w 1976 roku problem został rozwiązany przez Wolfganga Hakena i Kennetha Appela. Okazało się, że istotnie cztery kolory wystarczą do pomalowania dowolnej mapy. Dowód wymagał sprawdzenia 1936 przypadków, użyto do tego komputera. W późniejszych latach liczbę przypadków do sprawdzenia ograniczono do ok. 600.
Należy jednak podkreślić, że problem rozwiązali ludzie, a komputer tylko przyspieszył prace, sprawdzając skończoną liczbę przypadków. Nie jest prawdą (a takie wypowiedzi można czasem usłyszeć lub przeczytać), że „twierdzenie zostało udowodnione przez maszynę”, ani że dowodzenie twierdzeń matematycznych sprowadza się do rachunków na komputerze. Sposobów narysowania mapy na płaszczyźnie jest nieskończenie wiele. Dla komputera pojęcie nieskończoności nie istnieje, tym samym nie jest możliwe komputerowe sprawdzenie nieskończenie wielu przypadków.
Zdarza się natomiast sprowadzenie (oczywiście przez ludzi) problemu matematycznego do zbadania skończenie wielu przypadków. I dopiero w tym pomaga komputer.
Zachęcamy Czytelników do wydrukowania i samodzielnego pomalowania map administracyjnych Polski, Chin i Rosji, używając czterech kolorów. Mapy konturowe tych państw zamieszczamy w załączeniu.
Znajdźcie także przykłady map administracyjnych, do wykonania których wystarczy użyć mniej niż czterech kolorów.
Tekst: Krzysztof Kamiński
Bibliografia:
mimuw.edu.pl/delta/artykuly/delta0604/4barwy.pdf
https://en.wikipedia.org/wiki/Four_color_theorem
Źródła map znajdujących się w załączeniu:
Mapa Polski: http://commons.wikimedia.org/wiki/File:Poland_location_map_white.svg?uselang=pl
Mapa Chin: Jappalang,
http://commons.wikimedia.org/wiki/File:China_locator_map_(geographical_projection).svg?uselang=pl
Mapa Rosji: user:fremantleboy,
http://commons.wikimedia.org/wiki/File:Map_of_Russian_Subjects.svg?uselang=pl


